Here is a piece of music, which was composed with a sort of 17th century computer called the Organum Mathematicum, devised by Athanasius Kircher and fully described by his pupil and assistant Gaspar Schott:
It was the last post, touching on Robert Fludd’s Temple of Music, which reminded me of my interest in the Organum in around 2007, which is when the above piece was written. Now that I am free of the limitations of LiveJournal, I’d like to use this post to revisit Kircher and Schott’s work.

A surviving Organum Mathematicum (Museo Galileo)
The Organum, of which a surviving example is shown above, was essentially a wooden chest containing various wooden plates or ‘staves’ (baculi) upon which tables of data and rules were written. Originally built by Kircher as a pedagogical aid for the instruction of the 12-year-old Archduke Karl Joseph von Habsburg, it was fully described in Schott’s monumental, posthumous Organum Mathematicum : Libris IX Explicatum (1668). The various baculi contained therein can be used to plan fortified towns, calculate sundials, cipher messages, perform astronomical calculations, derive astrological data and compose music.
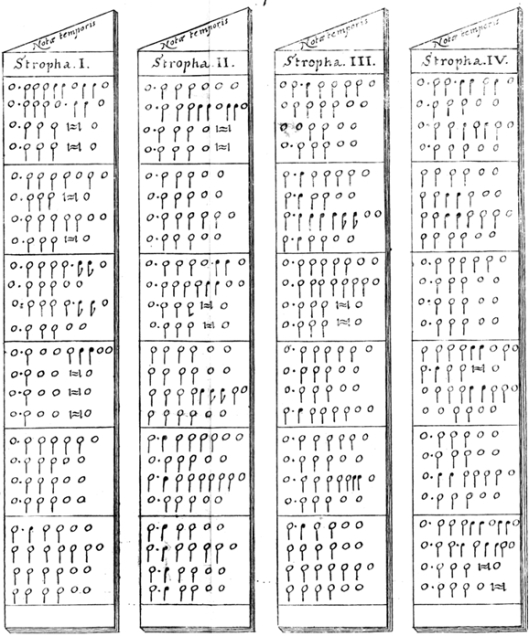
The Organum is essentially a variation on Kircher’s Arca Musarithma, a ‘mechanical’ composing tool proposed in the second volume of his Musurgia Universalis (1650). Here, the box contains various wooden staves containing details of toni (similar to our contemporary musical keys, and 12 in total) and various other staves, each one relating to a strophe (akin to a musical bar) of a certain number of syllables in length, the primary aim being to compose liturgical song, rather than instrumental music. The strophes could be assembled in various orders and, when mapped on to a given tonus, would yield a musical composition.
Schott presents a smaller set of toni and strophes, so that his Organum could include other disciplines, although what he does present is a useful summation of the Arca, which can be used to create compositions in both simple (or equal) and florid (or diminished) counterpoint. Kircher also provides guidance on modulating between toni over the course of a composition, as well as demonstrating his famed linguistic abilities by setting hymns in Greek, Hebrew, Arabic, Chaldean, and so on.
Below is a summary and discussion of the musical materials from the Organum, based on the work of Dr. H. J. Vollrath (University of Würzburg), who has created an extensive resource relating to Kircher’s invention (in German). I should also mention the work of creative programmer/polymath Jim Bumgardner, who began studying the music of the Organum in 2006. While revisiting this material, I was pleased to find that he had since written a paper on his software realisation of the Organum’s music. Jim also raises some interesting questions in his discussion, which would be worth pursuing in the future. In particular, the question of the ‘merit’ of the compositions produced by the Arca and Organum is an interesting one: they are, of course, all of a particular style, but perhaps we should also remember that prior to the Classical period, music often served a more functional and social role than an ‘high art’ one. Furthermore, anyone with a little knowledge of the rules could compose with the system, or follow other musical rules (for example, write a cantus firmus and then harmonise it), but these techniques are actually a small part of what making music of any lasting value is ‘about’.
What I personally find so pleasing about Kircher’s system is that it is inherently symbolic: the lines of counterpoint exist as abstract symbols (numbers), which may be mapped onto a multitude of tonalities and rhythms. This is very much the same way that I have approached the composition of algorithmic music, for example on the two albums recorded under the pseudonym Peter Cora (written with Symbolic Composer) or in my Spacious Mind project.
I. Composing simple (equal) counterpoint
Schott presents four sets of tables for composing simple counterpoint, which reflect the verse structure of various poetic meters. Having chosen a meter, the composer removes the four associated baculi from the box:

Archilochic baculi (reverse side of Sapphic baculi). NB: The toni listed should also include tonus VII – one of a number of typos in the engravings.
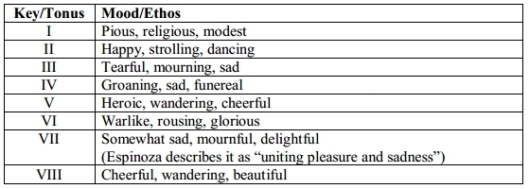
The next stage is to choose an appropriate tonus. At the top of each baculus, the applicable toni are listed – for example, the Archilochic meter can use toni V, VI and VIII. Each tonus has a specific ethos associated with it:
The baculus with the appropriate tonus is removed from the box and set in front of the composer. Note that some toni are marked as minor (molle) and in these cases the B is usually flattened. Additionally some other notes are also marked flat and sharp. These accidentals should be employed when the succeeding note either descends (e.g. in tonus II E-D becomes Eb-D) or when it rises by one semitone (e.g. in tonus II F-G becomes F#-G). Note also that in the minor toni, the Bb can also be ‘sharpened’ (e.g. made natural again) in similar circumstances.
Having chosen the meter and tonus, the composition can begin. Each meter has four baculi, one for each ‘strophe’ or line in the verse. Schott provides an example of setting Ave Maria stella in the Euripidean meter:
1. Looking at the baculus for the first strophe, choose one set of numbers. These numbers relate to the four voices (cantus/soprano, alto, tenor, bass). The first three voices can shuffled into any order, but the bass part must be unmoved. Schott picks this set:
2. A rhythmic scheme can now be chosen from the lower section. In this simple counterpoint one rhythm is applied to all the voices. There are two groups of schemes, for common and triple time. Schott’s example chooses 1/4. 1/8 1/4 1/4 1/2 1/2.
3. The tonus is now consulted and numbers mapped to pitches. Where accidentals are indicated, take these into account based on the tone that follows them. Note that the Bb has also been ‘sharpened’/naturalised in the given example. Schott does not (as far as I see) explain why: it seems most likely that the purpose is cadential (the last chord in many schools of counterpoint always being major), or perhaps because the cantus in the next strophe rises, or perhaps it also mirrors the harmonic rhythm established by the first three syllables?
The result may be notated thus:
II. Composing florid (diminished) counterpoint
The process for composing florid counterpoint is very much the same, and for this purpose Schott provides tables for the Euripidean and Archilochic modes. These baculi are double-sided – one side shows a series of tonal numbers, the other side a corresponding rhythmic schema:
Note that there are often more notes in these lines than syllables in the meter, therefore allowing the creation of melismatic passages. Schott provides the following example, again in tonus II:
Notated as:
III. Composing a cantus firmus with counterpoint
The final set of baculi move away from the combinatoric manipulation of large musical phrases and allow the composer to explore the setting of words in varying meters, based on the composition and then harmonisation of a bass voice. Schott gives the following example:
1. The text to be set is Laudate Dominum omnes gentes. It is divided into two groups: a six-syllable group (Laudate Dominum) and a four-syllable group (omnes gentes).
2. A single two-sided baculus is removed from the box, which shows various numerical and rhythmic fragments corresponding to syllabic counts – each has two species, one in which the penultimate syllable is longer than the final (syllaba pen. longa), and one in which it is shorter (syllaba pen. brev.).
Schott chooses the following numerical and rhythmic fragments:
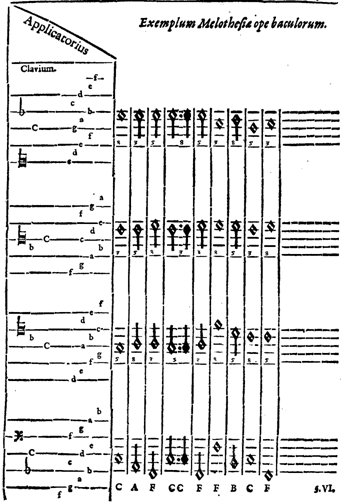
Which are mapped onto tonus VI:
3. The following baculi are now used to compose the counterpoint:
The bass voice is copied onto the appropriate staff on some manuscript paper. Next, for each note of the bass voice, the appropriate baculus is consulted. For each of the baculi, above bass staff, are shown staves for the other voices with a selection of notes indicated that can be chosen to create vertical harmonies with the bass voice. The numbers therefore indicate their relation to the bass note, e.g. a 3 indicates that note is a diatonic third above the bass. For each bass note, the numbers 3, 5 and 8 should be distributed between each of the three upper voices, while noting the following rules:
Care should be taken not to have two consecutive 5s or 8s – if this is the case then swap intervals with the voice below.
The voices should also be kept close together, avoiding wide intervals (e.g. more than an octave between parts), since they sound more harmonious this way.
Schott’s final composition of the phrase Laudate Dominum omnes gentes looks like this:
This method of simple harmonic counterpoint is somewhat similar to one demonstrated by Thomas Campion (1567-1620) in his treatise Of Making Foure Partes in Counterpoint [from p.81 in this PDF]. Campion uses this simple table to help composers make add counterpoint to a bass voice:
Jeff Lee wrote a brilliant explanation of how this contrapuntal method is applied – his website is now gone, but can be found via Archive.org. He applied the method to the bass voice of Orlando de Lasso’s O Occhi Manza Mia (published 1581) and found that the resulting counterpoint is exactly the same as in de Lasso’s original composition!
This partially answers Jim Bumgardner’s question about whether the music of the Organum was in vogue during the period: yes, and no. It was perhaps not the most cutting-edge music – the various species of counterpoint being codified since the early 16th century. However, akin to Robert Fludd’s Temple of Music (published 50 years prior to the Organum), this still reflected the fundamental principles of the compositional manuals of the time – Campion’s work, for example, was published by John Playford well into the 17th century.
Kircher & Schott’s contrapuntal baculi also remind me of a tool or compositional aide-memoire from Fludd’s Temple, which shows the harmonic relationships (thirds, fourths, fifths, octaves) across the gamut, which could also be used for the same purposes as the contrapuntal baculi:

Fludd’s harmonic gamut.
Phew. That was a long post! If you need more time to ponder these things, how about doing so while listening to this mix that I recently put together, presenting some recent and some perennial musical obsessions?






















magical.
Pingback: Omnium Gatherum: June 11th, 2014 | The Hermetic Library Blog
Pingback: Tradition and Innovation: Speculative Music and the Hexadic System | Larkfall
Pingback: Enquieriel & Co. – Selenus’ Musico-Angelic Cipher | Larkfall